Music Theory
It is important to note this section refers to music theory in general. The concept is the same for any instrument, the flute, the violin or guitar. I often refer to the guitar (frets, strings, etc.) because that is the instrument I teach. Knowing the concept of music theory will aid you in learning and progressing further with your music. Without even knowing theory as you progress with guitar you are using and learning parts of this music theory section.
The 12 Notes…
No matter what musical instrument you play, there are only twelve (12) notes that you can choose from. It is the combination and relations of these notes that make "music". These twelve notes, in order, are called the Chromatic Scale and if you play the notes or any portion of the scale in order (i.e. playing C,D,E,F) then you are said to be playing a Chromatic Progression.
When man first experimented with and started playing music, the system was called "Just Intonation". While this sufficed for simple instruments as music became more complex, the dissonance became more pronounced and music just sounded bad. In the late 1500's, the "Equal Temperament" system came into being. It is the Equal Temperament system that you and I play with today. Most western music, the stuff you and I play on the guitar utilize the "12 Tone Equal Temperament" scale.
What makes the notes we play sound good is the consonance of those notes (as opposed to the dissonance). The 12 Tone Equal Temperament scale is the only Equal Temperament scale that contains all seven intervals and more consonant intervals than dissonant intervals.
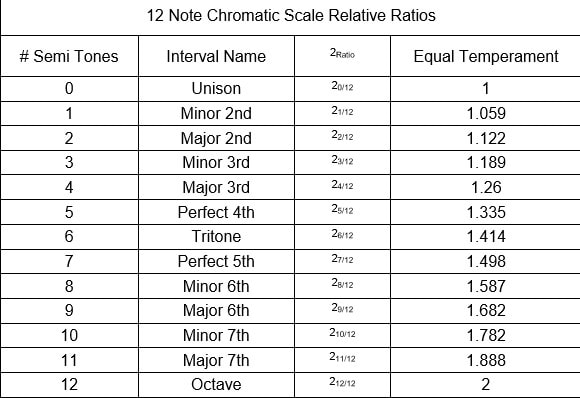
What makes the notes what they are? It is the ratio of the notes pitch to the first note of the scale. In our case, A is the first note.
Before I go on, you will have heard the term "tuned to 440" or "tuned to A440". What this means is that the A note we play is tuned to 440Hz (speed at which the note vibrates or oscillates). It is a fact that Human perception of pitch is logarithmic. This means that humans perceive equivalent pitches when they are separated by a factor of two. Therefore, humans would recognize the resonance of sound pitches oscillating at 220Hz, 440Hz and 880Hz (as an example).
When man first experimented with and started playing music, the system was called "Just Intonation". While this sufficed for simple instruments as music became more complex, the dissonance became more pronounced and music just sounded bad. In the late 1500's, the "Equal Temperament" system came into being. It is the Equal Temperament system that you and I play with today. Most western music, the stuff you and I play on the guitar utilize the "12 Tone Equal Temperament" scale.
What makes the notes we play sound good is the consonance of those notes (as opposed to the dissonance). The 12 Tone Equal Temperament scale is the only Equal Temperament scale that contains all seven intervals and more consonant intervals than dissonant intervals.
What makes the notes what they are? It is the ratio of the notes pitch to the first note of the scale. In our case, A is the first note.
Before I go on, you will have heard the term "tuned to 440" or "tuned to A440". What this means is that the A note we play is tuned to 440Hz (speed at which the note vibrates or oscillates). It is a fact that Human perception of pitch is logarithmic. This means that humans perceive equivalent pitches when they are separated by a factor of two. Therefore, humans would recognize the resonance of sound pitches oscillating at 220Hz, 440Hz and 880Hz (as an example).
Now what I said about western tuning standard being A440 because we tune A to 440Hz. Look at your guitar. Play the open A string. That is 440 Hz. If you play the low E string 5th fret, that is the exact same note or the same Octave as the open A string. They both oscillate at 440Hz. If you play the twelfth fret of the A string, also an A note, that is an Octave higher and is vibrating at 880 Hz. Play the A note on the D string (7th fret) and it is oscillating at 1760 Hz (a factor of 2 above the preceding octave).
Okay, so in the Equal Temperament scale the first note is a logarithmic progression (up or down) from 440Hz and we can move up and down octaves from that position based on ratios. Yes, the notes of the Chromatic scale are based on ratios that are relative to the first note. The exact formulas are shown in the table above.
For example, the 7th tone, the perfect 5th is obtained by multiplying the 12th root of 2 by itself, seven times. This gives us a ratio of 1.498. This means that a perfect fifth above A (the E note) is vibrating/oscillating at 659Hz. If you looked at the A note an Octave BELOW A440, then that A notes perfect 5th (also the E note) would be vibrating/oscillating at 330Hz.
Now, remember people (music teachers mostly) whining and complaining that you aren't playing the note close enough to the fret? If you play the note with your finger on the string right against the fret, you are applying the tension needed for that string to resonate at the proper frequency to form the note relative to it's ratio of vibration compared to the Unison. If you fret a string way back from the fret, you will change how fast that string vibrates (albeit slightly) and you won't be playing the exact note (not to mention the string buzz).
Okay, so in the Equal Temperament scale the first note is a logarithmic progression (up or down) from 440Hz and we can move up and down octaves from that position based on ratios. Yes, the notes of the Chromatic scale are based on ratios that are relative to the first note. The exact formulas are shown in the table above.
For example, the 7th tone, the perfect 5th is obtained by multiplying the 12th root of 2 by itself, seven times. This gives us a ratio of 1.498. This means that a perfect fifth above A (the E note) is vibrating/oscillating at 659Hz. If you looked at the A note an Octave BELOW A440, then that A notes perfect 5th (also the E note) would be vibrating/oscillating at 330Hz.
Now, remember people (music teachers mostly) whining and complaining that you aren't playing the note close enough to the fret? If you play the note with your finger on the string right against the fret, you are applying the tension needed for that string to resonate at the proper frequency to form the note relative to it's ratio of vibration compared to the Unison. If you fret a string way back from the fret, you will change how fast that string vibrates (albeit slightly) and you won't be playing the exact note (not to mention the string buzz).
Major Scale Construction...
.
If you remember from the lesson on Notes, these are the Twelve Notes of the Equal Temperament musical scale (the Chromatic Scale):
A - A# - B - C - C# - D - D# - E - F - F# - G - G#
Now, before we go any further in this lesson, there is something you must do. You need to memorize the following line. It will be used for as long as you play whatever instrument you wish to play. Memorize it now, this is the basis of music theory and will be needed moving forward.
Whole Step - Whole Step - Half Step - Whole Step - Whole Step - Whole Step - Half Step
( W-W-H-W-W-W-H )
Memorize it. If you prefer, the exact same thing may be expressed like this (memorize either one, it doesn't matter, just memorize at least ONE of them):
Tone - Tone - Semi Tone - Tone - Tone - Tone - Semi Tone
( W-W-H-W-W-W-H )
Got it memorized? Good. You now know everything you need to know to create any Major scale, on the spot, in your head.
Okay, okay. I'll explain it.
What are "Steps" and "Tones"
A Step is a reference to an Interval. A Tone is a reference to a difference in Pitch. However, for the guitar player, these mean basically the same thing.
For the guitar player, a WHOLE STEP is the distance between the first fret and two frets above it. Therefore moving from the 3rd fret (up two) to the 5th fret, is a Whole Step.
A Tone is the same thing. A full Tone to the guitar player, is two notes (frets) above the first Tone. Therefore, starting at the G note (3rd fret, Low E string) and moving up a full tone would put you on the A note (5th fret, Low E string).
So we can see that moving from G to G# to A is a whole tone difference and is ALSO a Whole Step difference.
On guitar a half step is one fret (a semi tone), a whole step (a whole tone) is two frets. Got it?
Now you are asking, so what is the difference between a G and a G# then? I'm glad you asked.
Moving from G to G# is moving one Semi Tone or Half Tone or one Fret, to put a fine point on it, a Half Step.
Got it? It's important.
Moving from A to A# is moving one Semi Tone/Half Step
Moving from A# to B is moving one Semi Tone/Half Step
Moving from B to C is moving one Semi Tone/Half Step
Moving from A to B is moving one Tone/Whole Step
Moving from B to C# is moving one Tone/Whole Step
Moving from C# to D# is moving one Tone/Whole Step
Make sure you understand Steps and Tones before you move on to Major scale construction.
Major Scale Construction
That thing I made you memorize above? That is the order you use to find the notes to construct a Major Scale. As our first example we will use the C Major Scale. I use the C Major Scale is because it is the most commonly used scale in music in the Western world. It is also the only Major scale that has all whole notes, no sharps or flats.
This is the C Major Scale:
C - D - E - F - G - A - B - C
Actually, the last C is simply the Octave of the Root note (or more accurately, the Octave of the Unison), it's just included to show how the Scale is circular (well, more spiral shaped than circular)
Constructing the C Major Scale
This is the way we construct the C Major scale. You will use this EXACT SAME METHOD to construct the other scales, you just use a different starting point. Major scales use 7 notes from the 12 note chromatic scale, built using the major scale formula we saw earlier.
The first thing we need is the 12 note Chromatic Scale (which is a no brainer, right?):
A - A# - B - C - C# - D - D# - E - F - F# - G - G#
Then we need the major scale formula I asked you to memorize:
( W-W-H-W-W-W-H )
So to create the C Major Scale we start with the note: C
(W): Now we move up the Chromatic Scale one WHOLE step/TONE (or two half steps, two semi-tones or TWO FRETS) and arrive at: D
(W): Now we move up the Chromatic Scale one WHOLE step/TONE (or two half steps, two semi-tones or TWO FRETS) and arrive at: E
(H): Now we move up the Chromatic Scale one HALF step/SEMI-tone (ONE FRET) and arrive at: F
(W): Now we move up the Chromatic Scale one WHOLE step/TONE (or two half steps, two semi-tones or TWO FRETS) and arrive at: G
(W): Now we move up the Chromatic Scale one WHOLE step/TONE (or two half steps, two semi-tones or TWO FRETS) and arrive at: A
(W): Now we move up the Chromatic Scale one WHOLE step/TONE (or two half steps, two semi-tones or TWO FRETS) and arrive at: B
(H): Now we move up the Chromatic Scale one HALF step/SEMI-tone (ONE FRET) and arrive at: C
Our C Major scale is complete. We applied the Major Scale Construction order of W-W-H-W-W-W-H to the Chromatic Scale from the starting point of the C note.
Let's Create the E Major Scale Using everything we have above:
A - A# - B - C - C# - D - D# - E - F - F# - G - G#
( W-W-H-W-W-W-H )
We can see exactly what we must do to create the E Major Scale:
1 One WHOLE step from E is F#
2 One WHOLE step from F# is G#
3 One HALF step from G# is A
4 One WHOLE step from A is B
5 One WHOLE step from B is C#
6 One WHOLE step from C# is D#
7 One HALF step from D# is E
Have you got the concept?
Your turn. Using the instructions above construct the G Major Scale, A Major Scale and D Major Scale. Write them in the boxes below.
G Major Scale: G __ __ __ __ __ __ __
A Major Scale: A __ __ __ __ __ __ __
D Major Scale: D __ __ __ __ __ __ __
Intervals…
For this section I RECOMMEND you have your guitar in hand so that you can finger the frets and play the Intervals while I am explaining them.
So far we've talked about notes and scales and have hinted at Intervals (whole step, half step, tone, semi-tone, fret). Now we will delve into Intervals and start understanding their names and how they work.
This is the Chromatic Scale:
A - A# - B - C - C# - D - D# - E - F - F# - G - G#
Now, we add the A note to the end, so that we are spiraling back to where we start, still have the Chromatic Scale (and use this one for the rest of the lesson):
If you remember from the lesson on Notes, these are the Twelve Notes of the Equal Temperament musical scale (the Chromatic Scale):
A - A# - B - C - C# - D - D# - E - F - F# - G - G#
Now, before we go any further in this lesson, there is something you must do. You need to memorize the following line. It will be used for as long as you play whatever instrument you wish to play. Memorize it now, this is the basis of music theory and will be needed moving forward.
Whole Step - Whole Step - Half Step - Whole Step - Whole Step - Whole Step - Half Step
( W-W-H-W-W-W-H )
Memorize it. If you prefer, the exact same thing may be expressed like this (memorize either one, it doesn't matter, just memorize at least ONE of them):
Tone - Tone - Semi Tone - Tone - Tone - Tone - Semi Tone
( W-W-H-W-W-W-H )
Got it memorized? Good. You now know everything you need to know to create any Major scale, on the spot, in your head.
Okay, okay. I'll explain it.
What are "Steps" and "Tones"
A Step is a reference to an Interval. A Tone is a reference to a difference in Pitch. However, for the guitar player, these mean basically the same thing.
For the guitar player, a WHOLE STEP is the distance between the first fret and two frets above it. Therefore moving from the 3rd fret (up two) to the 5th fret, is a Whole Step.
A Tone is the same thing. A full Tone to the guitar player, is two notes (frets) above the first Tone. Therefore, starting at the G note (3rd fret, Low E string) and moving up a full tone would put you on the A note (5th fret, Low E string).
So we can see that moving from G to G# to A is a whole tone difference and is ALSO a Whole Step difference.
On guitar a half step is one fret (a semi tone), a whole step (a whole tone) is two frets. Got it?
Now you are asking, so what is the difference between a G and a G# then? I'm glad you asked.
Moving from G to G# is moving one Semi Tone or Half Tone or one Fret, to put a fine point on it, a Half Step.
Got it? It's important.
Moving from A to A# is moving one Semi Tone/Half Step
Moving from A# to B is moving one Semi Tone/Half Step
Moving from B to C is moving one Semi Tone/Half Step
Moving from A to B is moving one Tone/Whole Step
Moving from B to C# is moving one Tone/Whole Step
Moving from C# to D# is moving one Tone/Whole Step
Make sure you understand Steps and Tones before you move on to Major scale construction.
Major Scale Construction
That thing I made you memorize above? That is the order you use to find the notes to construct a Major Scale. As our first example we will use the C Major Scale. I use the C Major Scale is because it is the most commonly used scale in music in the Western world. It is also the only Major scale that has all whole notes, no sharps or flats.
This is the C Major Scale:
C - D - E - F - G - A - B - C
Actually, the last C is simply the Octave of the Root note (or more accurately, the Octave of the Unison), it's just included to show how the Scale is circular (well, more spiral shaped than circular)
Constructing the C Major Scale
This is the way we construct the C Major scale. You will use this EXACT SAME METHOD to construct the other scales, you just use a different starting point. Major scales use 7 notes from the 12 note chromatic scale, built using the major scale formula we saw earlier.
The first thing we need is the 12 note Chromatic Scale (which is a no brainer, right?):
A - A# - B - C - C# - D - D# - E - F - F# - G - G#
Then we need the major scale formula I asked you to memorize:
( W-W-H-W-W-W-H )
So to create the C Major Scale we start with the note: C
(W): Now we move up the Chromatic Scale one WHOLE step/TONE (or two half steps, two semi-tones or TWO FRETS) and arrive at: D
(W): Now we move up the Chromatic Scale one WHOLE step/TONE (or two half steps, two semi-tones or TWO FRETS) and arrive at: E
(H): Now we move up the Chromatic Scale one HALF step/SEMI-tone (ONE FRET) and arrive at: F
(W): Now we move up the Chromatic Scale one WHOLE step/TONE (or two half steps, two semi-tones or TWO FRETS) and arrive at: G
(W): Now we move up the Chromatic Scale one WHOLE step/TONE (or two half steps, two semi-tones or TWO FRETS) and arrive at: A
(W): Now we move up the Chromatic Scale one WHOLE step/TONE (or two half steps, two semi-tones or TWO FRETS) and arrive at: B
(H): Now we move up the Chromatic Scale one HALF step/SEMI-tone (ONE FRET) and arrive at: C
Our C Major scale is complete. We applied the Major Scale Construction order of W-W-H-W-W-W-H to the Chromatic Scale from the starting point of the C note.
Let's Create the E Major Scale Using everything we have above:
A - A# - B - C - C# - D - D# - E - F - F# - G - G#
( W-W-H-W-W-W-H )
We can see exactly what we must do to create the E Major Scale:
1 One WHOLE step from E is F#
2 One WHOLE step from F# is G#
3 One HALF step from G# is A
4 One WHOLE step from A is B
5 One WHOLE step from B is C#
6 One WHOLE step from C# is D#
7 One HALF step from D# is E
Have you got the concept?
Your turn. Using the instructions above construct the G Major Scale, A Major Scale and D Major Scale. Write them in the boxes below.
G Major Scale: G __ __ __ __ __ __ __
A Major Scale: A __ __ __ __ __ __ __
D Major Scale: D __ __ __ __ __ __ __
Intervals…
For this section I RECOMMEND you have your guitar in hand so that you can finger the frets and play the Intervals while I am explaining them.
So far we've talked about notes and scales and have hinted at Intervals (whole step, half step, tone, semi-tone, fret). Now we will delve into Intervals and start understanding their names and how they work.
This is the Chromatic Scale:
A - A# - B - C - C# - D - D# - E - F - F# - G - G#
Now, we add the A note to the end, so that we are spiraling back to where we start, still have the Chromatic Scale (and use this one for the rest of the lesson):
A - A# - B - C - C# - D - D# - E - F - F# - G - G# - A
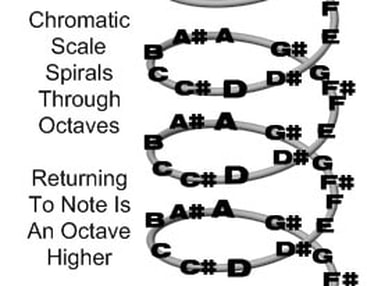
There are twelve notes in the Chromatic Scale plus the Root note, an octave higher. A few times I have said the Chromatic Scale "spirals" back to the Root Note, an octave higher. I hope this simple graphic helps illustrate it. Do not EVER think that a scale is "circular". Scales are not circular, scales "Spiral". Each time you encounter the Root note, you are an Octave higher or lower, depending on which way you travelled.
There are twelve notes in the Chromatic Scale plus the Root note, an octave higher. A few times I have said the Chromatic Scale "spirals" back to the Root Note, an octave higher. I hope this simple graphic helps illustrate it. Do not EVER think that a scale is "circular". Scales are not circular, scales "Spiral". Each time you encounter the Root note, you are an Octave higher or lower, depending on which way you travelled.
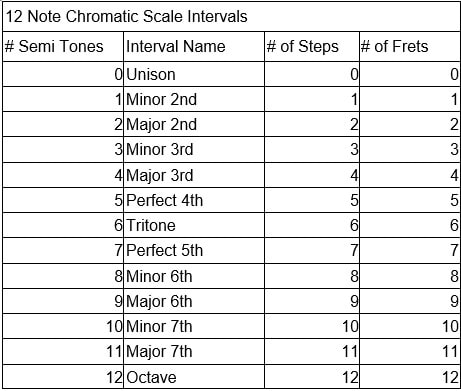
Now, back to the Chromatic scale with the "Octave" added. This scale has twelve (12) Intervals.
There "Intervals" are the "Spaces Between The Notes" for want of a better definition. More precisely, an Interval is the MOVEMENT ACROSS THE SPACE BETWEEN THE NOTES
When we move from A to A# we moved across the one space between two adjacent notes. That is to say, we moved one interval. Moving that one interval has a name. It is called a Minor 2nd, more on that later.
There "Intervals" are the "Spaces Between The Notes" for want of a better definition. More precisely, an Interval is the MOVEMENT ACROSS THE SPACE BETWEEN THE NOTES
When we move from A to A# we moved across the one space between two adjacent notes. That is to say, we moved one interval. Moving that one interval has a name. It is called a Minor 2nd, more on that later.
Understanding the Octave is important. I just want you to understand that when I refer to "THE Octave" I am refering to a note twelve intervals higher. When I talk about "AN Octave", I am talking about a range of twelve intervals.
So, moving from A to A# is one interval. Moving from C# to D and moving from E to F is one interval. Moving from one note to the next adjacent note is one interval.
Therefore, building on this idea, moving from one note to the second note away is moving two intervals. So, moving from A to B is moving two intervals. Moving from B to C# is moving two intervals. Got it? Move one note adjacent is one interval and move two notes adjacent is two intervals. Yes, moving two intervals has a name. It is a Major 2nd. More on that later.
Unison:
The Unison needs a little bit of explaining. When you are use the term "Unison" you are referring to the first note in the scale. For example, in the C Major Scale, the FIRST "C" note you play is the Unison for the C Major Scale. The SECOND C you play (on the spiral) is the Octave.
Making sense of the names
Before we move along it is important to simplify this concept. Each of the 12 steps has a name, these names never change, but the notes they refer to do depending on specifically what note you start on.
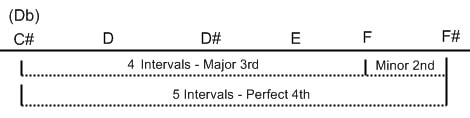
So I'm playing my guitar with some friends. We have been has trying to work out a riff for a new song. The guitarist needs some help so he says to me, "Hey man, Give me a D flat". So I do. I play the 9th fret of the low E string. Then he says, "Nah that's not it, give me a Major 3rd above". Because I know my Chromatic Scale and I know that a Major 3rd is four intervals, I play the 4th string 3rd fret which is F. He says, "That's almost it, make it a Perfect 4th.". So I do. One more interval above the Major 3rd is a Perfect 4th. I move my hand one fret and play an F# on the 4th string 4th fret.
Okay, that might have thrown you off a bit. When asked for the D flat (Db) you probably said, WAIT a minute. There are no flat D's on the Chromatic Scale!
You can sharpe and flat most notes in the Chromatic scale by moving one HALF step (one fret) in the required direction. Therefore, to make D sharp (D#), I move up a fret and get D#. To make D flat (Db) I move down a fret and I get Db. HOWEVER, what you see when you look at the Chromatic Scale above is that one fret down (one half step, one semi-tone) is actually C#.
You see, the note BETWEEN the note C and the note D is both C# and Db. The only exceptions to this are that there is no Cb and there is no Fb. That is because one half step down from C is the note B and one half step down from the note F is the note E.
Memorize this - there is no sharp (or flat) between B and C and between E and F.
Moving right along.....
Referring back to my earlier situation with in the garage...
He asked me for a Db and I gave it to him. He then asked for a Major 3rd. What he actually said was "play the note four intervals higher than the note I asked you to play before". I know from my studies of Music Theory and application of said theory to the guitar fretboard that four intervals equals four frets AND equals four notes. Playing either the Low E string 13th fret OR the A string 3rd fret are four intervals ABOVE the original note, the DB (remember what I said about the Unison of the Unison? That is why I got to choose HOW I was going to play the Major 2nd).
When he said to me make it a Perfect 4th, I knew from my blah blah blah that he was actually asking me to play "the fifth interval above the note I originally asked you to play". Because I was now playing a Perfect 4th instead of a Major 3rd I knew that in simpler terms I was playing FIVE semi-tones (frets) instead of FOUR semi-tones (frets) above what I had originally played. Therefore, through the astounding powers of my deductive reasoning, I subtracted 4 (Major 3rd) from 5 (Perfect 4th) and wound up with 1 (Minor 2nd). So what I had done was deduced that I only needed to move ONE MORE FRET (semi-tone) to turn that Major 3rd into a Perfect 4th. So that's what I did, I moved one fret or more geeky speaking, I increased the Major 3rd by a Minor 2nd.
Making MORE sense of the names
Let's look at the G Major Scale:
G - A - B - C - D - E - F# - G
The Unison is "G". Right? Okay.
The next note in the G Major scale is "A". However, the note "A" is TWO INTERVALS (a tone, a whole step, two frets) from the Unison. Since it is TWO INTERVALS from the Unison I know that in the G Major Scale the next note, the A, is a Major 2nd.
The note AFTER the A is the B note. The B note is FOUR INTERVALS away from the Unison. (G to G#, G# to A, A to A#, A# to B). Therefore, I know the name for FOUR INTERVALS (2+2) from the Unison and can say that in the G Major Scale the note B is a Major 3rd.
The note AFTER the B is the C note. We will remember from the Intervals of the Major Scale (WWHWWWH) that the next note, the "C" note is a HALF STEP above "B". Therefore since it is FIVE INTERVALS (2+2+1) from the Unison I can say that in the G Major Scale the note C is a Perfect 4th.
The note AFTER the C is the D note. We will remember from the Intervals of the Major Scale (WWHWWWH) that the next note, the "D" note is a WHOLE STEP above "C". Therefore since it is SEVEN INTERVALS (2+2+1+2) from the Unison I can say that in the G Major Scale the note D is a Perfect 5th.
The note AFTER the D is the E note. We will remember from the Intervals of the Major Scale (WWHWWWH) that the next note, the "E" note is a WHOLE STEP above "D". Therefore since it is NINE INTERVALS (2+2+1+2+2) from the Unison I can say that in the G Major Scale the note E is a Major 6th.
The note AFTER the E is the F# note. We will remember from the Intervals of the Major Scale (WWHWWWH) that the next note, the "F#" note is a WHOLE STEP above "E". Therefore since it is ELEVEN INTERVALS (2+2+1+2+2+2) from the Unison I can say that in the G Major Scale the note F# is a Major 7th.
The note AFTER the F# is the G note. We will remember from the Intervals of the Major Scale (WWHWWWH) that the next note, the "G" note is a HALF STEP above "F#". Therefore since it is TWELVE INTERVALS (2+2+1+2+2+2+1) from the Unison I can say that in the G Major Scale the NEXT note G is an Octave.
Showing Intervals on the guitar
It's all relative
It is important that when you are talking about Intervals, you know what note you are starting FROM in reference to the Intervals, or more specifically, what note the Interval is in reference to.
The reason being, looking above, we know that the note D in the G Major Scale is a Perfect 5th above the Unison or more simply, a Perfect 5th. HOWEVER....
In the G Major Scale, the note "E" is a Perfect 5th above the note A. This is because there are SEVEN INTERVALS between A and E:
G - A - B - C - D - E - F# - G
The Unison is "G". Right? Okay.
The next note in the G Major scale is "A". However, the note "A" is TWO INTERVALS (a tone, a whole step, two frets) from the Unison. Since it is TWO INTERVALS from the Unison I know that in the G Major Scale the next note, the A, is a Major 2nd.
The note AFTER the A is the B note. The B note is FOUR INTERVALS away from the Unison. (G to G#, G# to A, A to A#, A# to B). Therefore, I know the name for FOUR INTERVALS (2+2) from the Unison and can say that in the G Major Scale the note B is a Major 3rd.
The note AFTER the B is the C note. We will remember from the Intervals of the Major Scale (WWHWWWH) that the next note, the "C" note is a HALF STEP above "B". Therefore since it is FIVE INTERVALS (2+2+1) from the Unison I can say that in the G Major Scale the note C is a Perfect 4th.
The note AFTER the C is the D note. We will remember from the Intervals of the Major Scale (WWHWWWH) that the next note, the "D" note is a WHOLE STEP above "C". Therefore since it is SEVEN INTERVALS (2+2+1+2) from the Unison I can say that in the G Major Scale the note D is a Perfect 5th.
The note AFTER the D is the E note. We will remember from the Intervals of the Major Scale (WWHWWWH) that the next note, the "E" note is a WHOLE STEP above "D". Therefore since it is NINE INTERVALS (2+2+1+2+2) from the Unison I can say that in the G Major Scale the note E is a Major 6th.
The note AFTER the E is the F# note. We will remember from the Intervals of the Major Scale (WWHWWWH) that the next note, the "F#" note is a WHOLE STEP above "E". Therefore since it is ELEVEN INTERVALS (2+2+1+2+2+2) from the Unison I can say that in the G Major Scale the note F# is a Major 7th.
The note AFTER the F# is the G note. We will remember from the Intervals of the Major Scale (WWHWWWH) that the next note, the "G" note is a HALF STEP above "F#". Therefore since it is TWELVE INTERVALS (2+2+1+2+2+2+1) from the Unison I can say that in the G Major Scale the NEXT note G is an Octave.
Showing Intervals on the guitar
It's all relative
It is important that when you are talking about Intervals, you know what note you are starting FROM in reference to the Intervals, or more specifically, what note the Interval is in reference to.
The reason being, looking above, we know that the note D in the G Major Scale is a Perfect 5th above the Unison or more simply, a Perfect 5th. HOWEVER....
In the G Major Scale, the note "E" is a Perfect 5th above the note A. This is because there are SEVEN INTERVALS between A and E:
Point of Confusion...
You need to keep in mind the CHROMATIC scale when you are talking about INTERVALS and not the MAJOR SCALE.
The most common mistake you will make at this point is to look at the Major Scale and count the notes as one interval each. You need to keep in mind that the Chromatic Scale has ALL the notes and ALL the Intervals where the Major Scale has SOME of the notes AND ALL OF THE INTERVALS.
Always have the CHROMATIC scale in your mind when you are talking ABOUT Intervals and use the Major Scale as the reference to the Unison
You need to keep in mind the CHROMATIC scale when you are talking about INTERVALS and not the MAJOR SCALE.
The most common mistake you will make at this point is to look at the Major Scale and count the notes as one interval each. You need to keep in mind that the Chromatic Scale has ALL the notes and ALL the Intervals where the Major Scale has SOME of the notes AND ALL OF THE INTERVALS.
Always have the CHROMATIC scale in your mind when you are talking ABOUT Intervals and use the Major Scale as the reference to the Unison
ALMOST DONE!
I'm almost done with this section. I just want to summarize some important points for you to remember (in no particular order):
1. ONE Interval is ONE Fret
2. ONE Interval is a HALF Step
3. ONE Interval is a SEMI-Tone
4. TWO INTERVALS is TWO Frets
5. TWO INTERVALS is a WHOLE Step
6. TWO INTERVALS is a TONE
7. There are TWELVE Intervals in the CHROMATIC Scale.
8. There are TWELVE Intervals in the Major Scale (you just don't talk about all of them).
9. The Interval can ONLY be expressed RELATIVE TO A STARTING Note.
If I said to Tony Iommi, without reference to anything else, "Hey Tony, play a Perfect 5th" he would slap me and Ozzy would hurt himself laughing. However, if I said to Tony, "Hey Tony, I'm playing in G, can you give me a Perfect 5th?", then we'd be rocking and rolling.
10. Knowing what intervals are and what they do is FAR more important than knowing the names of the Intervals.
11. Do yourself a favor, start learning the names of the Intervals. You will use them forever.
12. A two note Power Chord is the Root note and a Perfect 5th. (More on that soon)
13. A three note Power Chord is the Root note, a Perfect 5th and a Perfect 4th above the 5th (which is to say, an Octave above the Unison). (More on that soon.... see how important understanding Intervals is?)
I'm almost done with this section. I just want to summarize some important points for you to remember (in no particular order):
1. ONE Interval is ONE Fret
2. ONE Interval is a HALF Step
3. ONE Interval is a SEMI-Tone
4. TWO INTERVALS is TWO Frets
5. TWO INTERVALS is a WHOLE Step
6. TWO INTERVALS is a TONE
7. There are TWELVE Intervals in the CHROMATIC Scale.
8. There are TWELVE Intervals in the Major Scale (you just don't talk about all of them).
9. The Interval can ONLY be expressed RELATIVE TO A STARTING Note.
If I said to Tony Iommi, without reference to anything else, "Hey Tony, play a Perfect 5th" he would slap me and Ozzy would hurt himself laughing. However, if I said to Tony, "Hey Tony, I'm playing in G, can you give me a Perfect 5th?", then we'd be rocking and rolling.
10. Knowing what intervals are and what they do is FAR more important than knowing the names of the Intervals.
11. Do yourself a favor, start learning the names of the Intervals. You will use them forever.
12. A two note Power Chord is the Root note and a Perfect 5th. (More on that soon)
13. A three note Power Chord is the Root note, a Perfect 5th and a Perfect 4th above the 5th (which is to say, an Octave above the Unison). (More on that soon.... see how important understanding Intervals is?)
Minor Scale Construction
The minor scale (also called Aeolian) is a major scale with its 3rd, 6th, and 7th degrees flattened.
As we saw in the previous lesson (major scales), the placement of tones and semi-tones is what gives each type of scale its individual sound.
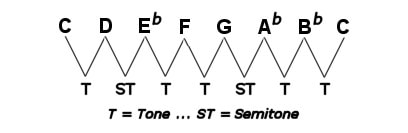
If we take the C Major scale and flatten the 3rd, 6th, and 7th degrees, we get the following placement of tones and semi-tones.
The minor scale (also called Aeolian) is a major scale with its 3rd, 6th, and 7th degrees flattened.
As we saw in the previous lesson (major scales), the placement of tones and semi-tones is what gives each type of scale its individual sound.
If we take the C Major scale and flatten the 3rd, 6th, and 7th degrees, we get the following placement of tones and semi-tones.
If you were to start on any note and apply this order of tones and semi-tones ( T, ST, T, T, ST, T, T) you would end up playing a minor scale.
Parallel and Relative Minor Scales
Parallel minor scales start on the same note as their major scale counterparts. In the above example, the C minor scale started on the same note as the C Major scale. Therefore the C minor scale is the parallel minor of C major.
Relative minor scales start from the 6th degree (or 6th note) of the major scale.
For example, A minor is the relative minor of C major.
C major C D E F G A B C
A minor A B C D E F G A
In the last lessons, you have seen that the major scale is also known as Ionian and that the minor scale is also known as Aeolian. In upcoming lessons, we will further explore all of the related scales called modes.
Parallel and Relative Minor Scales
Parallel minor scales start on the same note as their major scale counterparts. In the above example, the C minor scale started on the same note as the C Major scale. Therefore the C minor scale is the parallel minor of C major.
Relative minor scales start from the 6th degree (or 6th note) of the major scale.
For example, A minor is the relative minor of C major.
C major C D E F G A B C
A minor A B C D E F G A
In the last lessons, you have seen that the major scale is also known as Ionian and that the minor scale is also known as Aeolian. In upcoming lessons, we will further explore all of the related scales called modes.
Relative Minor and Major Scales
Relative minor scale is really used in improvisation, because it gives more ideas to solo. All improviser that learned to use major and minor scales have to learn, after that, to use the relative minor scale. But what is the relative minor scale?
Example of relative minor scale
Think in some major scale, for example, C major scale. The C relative minor scale will be A minor scale. As a rule, the relative minor scale of a major scale is the minor scale of the sixth degree of this tonality. Saying this way may look confuse, but is really simple in practice. As we were in C, the sixth degree is A, so is just play A minor scale.
Observation: if you are still lost about degrees, read again the article “degrees and music intervals”.
Well, as you can see, we are not learning any new scale here. This scale is nothing more than the natural minor scale that we already saw. Only creating a link of sixth degree in relation to the first, and then you will understand this.
Relationship between major scale and relative minor scale
If you take C major scale and compare it to A minor scale, you will see that they have exactly the same notes. In other words, the major scale has a related minor that is identical to it. Incredible, isn’t it? This is why the name “relative”. Compare below, for example, the scales
C x Am and G x Em:
• C major scale: C, D, E, F, G, A, B
• A minor scale: A, B, C, D, E, F, G
• G major scale: G, A, B, C, D, E, F#
• E minor scale: E, F#, G, A, B, C
This is extremely useful! It means that we can use A minor scale to do a solo in a song which tonality is C major. In other words, when we have a major tonality, we can think in two scales: the major scale of this tonality and the relative minor scale of it. This increases our options when we are thinking in solo.
Relative major
In the same way, we could think in the opposite: each minor tonality has a relative major. This major relative is located a tone and a half above the minor tonality. For example, one tone and a half above A is C. Therefore, the relative major of A minor is C major.
Relative minor chord
It is worth to highlight that this concept also exists to the chords. The relative minor chord is the chord of sixth degree of major chord in question. For example, the relative minor of C is the chord of sixth degree in the harmonic field of C major, in other words, A minor. Other example: suppose that the tonality be G major. The relative minor of G will be E.
As the relative chords have affinity among them, they can substitute one another. We will see this with more details in the study of harmonic functions. For now, think in scales; remember that you can always use a relative minor with a major scale.
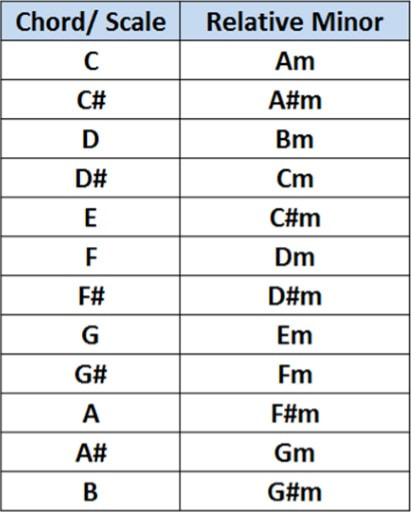
Try to test this taking a song in a major tonality and playing the relative minor on it. You will see as it fits perfectly. Now that you already learned what you needed about relative minor, try to find the relative minor of all the other chords or major scales. After that, check with the table below:
Relative minor scale is really used in improvisation, because it gives more ideas to solo. All improviser that learned to use major and minor scales have to learn, after that, to use the relative minor scale. But what is the relative minor scale?
Example of relative minor scale
Think in some major scale, for example, C major scale. The C relative minor scale will be A minor scale. As a rule, the relative minor scale of a major scale is the minor scale of the sixth degree of this tonality. Saying this way may look confuse, but is really simple in practice. As we were in C, the sixth degree is A, so is just play A minor scale.
Observation: if you are still lost about degrees, read again the article “degrees and music intervals”.
Well, as you can see, we are not learning any new scale here. This scale is nothing more than the natural minor scale that we already saw. Only creating a link of sixth degree in relation to the first, and then you will understand this.
Relationship between major scale and relative minor scale
If you take C major scale and compare it to A minor scale, you will see that they have exactly the same notes. In other words, the major scale has a related minor that is identical to it. Incredible, isn’t it? This is why the name “relative”. Compare below, for example, the scales
C x Am and G x Em:
• C major scale: C, D, E, F, G, A, B
• A minor scale: A, B, C, D, E, F, G
• G major scale: G, A, B, C, D, E, F#
• E minor scale: E, F#, G, A, B, C
This is extremely useful! It means that we can use A minor scale to do a solo in a song which tonality is C major. In other words, when we have a major tonality, we can think in two scales: the major scale of this tonality and the relative minor scale of it. This increases our options when we are thinking in solo.
Relative major
In the same way, we could think in the opposite: each minor tonality has a relative major. This major relative is located a tone and a half above the minor tonality. For example, one tone and a half above A is C. Therefore, the relative major of A minor is C major.
Relative minor chord
It is worth to highlight that this concept also exists to the chords. The relative minor chord is the chord of sixth degree of major chord in question. For example, the relative minor of C is the chord of sixth degree in the harmonic field of C major, in other words, A minor. Other example: suppose that the tonality be G major. The relative minor of G will be E.
As the relative chords have affinity among them, they can substitute one another. We will see this with more details in the study of harmonic functions. For now, think in scales; remember that you can always use a relative minor with a major scale.
Try to test this taking a song in a major tonality and playing the relative minor on it. You will see as it fits perfectly. Now that you already learned what you needed about relative minor, try to find the relative minor of all the other chords or major scales. After that, check with the table below: